COVID-19の感染の脅威は、「デルタ株」の拡大とともに続いています。この中で、「感染防止と経済活動のどちらを優先すべきか」に関する論争も終わる気配がありません。
もちろん、単純な答えは「どちらも大事」なのですが、これは「役に立つ答え」にはなりません。経済活動は人と人との関わり合いから生まれるものですので、感染防止と経済活動との間にはトレードオフが避けられません。一人一人が部屋に閉じこもり絶対に他人と接触しなければ、感染は防げますが経済活動も維持できなくなります。一方、人と人との接触に何の制約もかけなければ、経済活動は維持できても感染は拡がります。最適な解はその中間のどこかにあるのでしょうが、その場所を探り当てるのは至難の業です。人命という本質的に“Priceless”なものと経済価値との比較には、どうしても各人の価値観が反映されますし、日々刻々変化する状況にも大きく左右されるからです。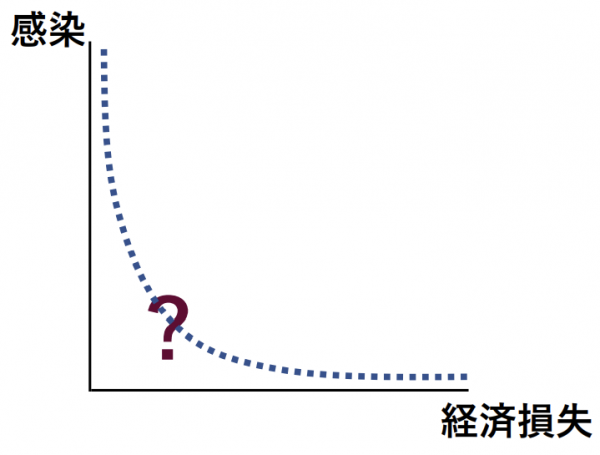
シンプルなモデルを手掛かりに
感染症の動向を予測するための、よく知られるシンプルなモデルは、「SIR モデル」と呼ばれるものです（モデルの概要にご関心のある方は、後述の別添をお読みください）。
このモデルでは、先行きの感染者比率は、現時点での「非感染者比率」に「感染者比率」を乗じ、さらに「基本再生産数」を乗じたものに左右されると捉えられます。この「基本再生産数（Basic Reproduction Number, R0と表されることが多い）」とは、「免疫を持たない集団に入り込んだ感染者１人が、回復するまでに何人に感染させるか」を示す値です。この値は、病原体そのものの感染力や、人と人との接触頻度によって決まります。
また、「非感染者比率」と「感染者比率」を乗じるのは、直感的にも理解しやすいでしょう。非感染者比率が100％（すなわち、感染者がゼロ）なら感染は起こらず、一方で、非感染者比率が0%（すなわち、全員が感染済み）になってしまうと、もうそれ以上感染は広がりようがないからです。
この基本再生産数が１を大きく上回れば、新たに増えた感染者が、非感染者をさらに感染させやすくするため、急速に感染が広まりやすくなります。一方で、基本再生産数が１を下回れば、計算上、感染は徐々に収束していくことになります。
（なお、「免疫を持たない集団」ではなく、すでに感染者が出ている環境での特定の時点tにおいて、感染者一人が何人に感染させるかを示す値は、「実効再生産数（Effective Reproduction Number）」と呼ばれ、Rtと表されます。これも感染抑制にとって重要な目安となる値ですが、この値は時点によって変動するため、議論をシンプルにする観点から、本稿では「基本再生産数」に絞って記述することとします。）
したがって、「基本再生産数が１を下回る所まで人と人との接触を減らそう」と考えることは、対応としては自然です。しかし、現実の政策判断においてどの程度の行動制限をかければ良いのか、モデルから導き出すことは容易ではありません。
経済分析に長らく従事し、さまざまなモデルを見てきた立場からみて、このモデルの特徴は「基本再生産数」に推計値が大きく左右される点にあります。
基本再生産数の前提と推計値との関係例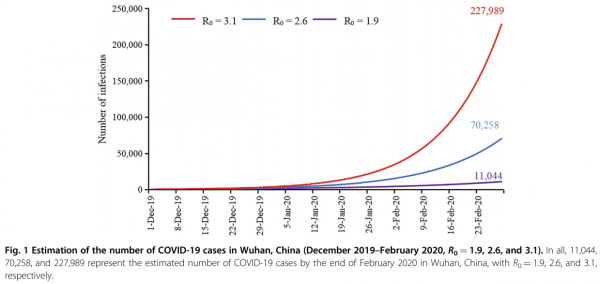
©️ Wang et al. Cell Discovery (2020)
https://www.nature.com/articles/s41421-020-0148-0.pdf
基本再生産数が既知、かつ不変であれば良いのですが、現実のウイルスは変異を繰り返します。この結果生じる「基本再生産数」の振れと不確実性は、そのまま推計値に大きな不確実性をもたらします。したがって、ここから導き出される推計値は、本来、相当な幅をもってみるべきものです。
政策対応の経済への影響
そのうえで、最近よく分析に使われる、レストラン予約サイト”Open Table”のレストラン予約状況から、政策対応との関係を見てみましょう。これを見ると、国によって対応はかなりまちまちであり、また、どの国の対応が優れているとも言い切れないことが窺われます。
“Open Table”によるレストラン予約件数前年比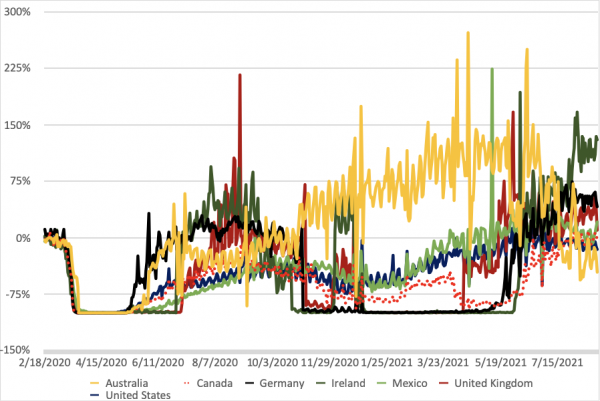
出所：Open Table（異常値を一部筆者が修正）
例えば、ぎりぎりまで厳しいロックダウンを行った国々（典型的には英国、アイルランド）では、ロックダウン解除後のレストラン予約の回復が急激になる傾向がみられます。もっとも、その後感染が再び拡大し、再び厳しいロックダウンへの移行を余儀なくされています。
データの共有とモデルの限界への理解
これらの例が示すように、経済分析と感染症分析がオーバーラップする分野では、なお、未知の領域が大きいのです。
経済予測に携わったエコノミストの多くは、過去の経済データの動きを見事に説明できそうなモデルを見つけて小躍りした経験があると思います。しかし、このような関係式は殆どの場合、新しいデータが入るにつれて説明力を失っていきます。現実の経済はモデルよりもはるかに複雑ですし、絶えず構造変化を起こしているからです。これは感染症のモデルにも当てはまります。メディアでは往々にして、断定的な物言いをするコメンテーターが重宝されがちですが、モデルに依拠して「経済状況、あるいは感染状況は必ずこうなる」と主張する言説には、相当注意した方が良いでしょう。
そのうえで、経済分析でも感染症分析でも、①入手可能なデータを極力共有すること、②モデルの限界を十分理解すること、③誤りの経験を活かすこと、が生産的な議論を行う上で重要です。予測を誤った人々がその後沈黙しがちであることは否めませんが、「このような前提をもとにこう試算したら、現実の値とこれだけ外れた」という経験の共有は、分析手法の進歩のために重要な情報となり得ます。
また、データの共有については、日本を含む多くの国々で、COVID-19の経験が、「データを公開し共有しなければならない」という認識を大きく広めた面はあると思います。これまで人類が経験した感染症の中で、COVID-19ほど多くの関連データが収集され、公開されたケースはないでしょう。今回の経験が、データの重要性に関する認識の浸透とその有益な活用につながることを願いたいと思います。
（別 添）SIRモデル
「SIRモデル」の名称は、未感染者（Susceptible）、感染者（Infected）、回復者（Recovered）の頭文字を繋ぎ合わせたものです（なお、回復者には亡くなられた方（Dead, D）を含みます）。
一国の総人口をNとすると、未感染者、感染者、回復者のいずれかに分類できますので、以下のように表せます。
N（総人口）＝S（未感染者数）+I（感染者数）+R（回復者数）
回復者数（R）は、感染者数（I）の数に、感染者が回復するか亡くなる確率を掛けた数だけ変化します。この確率をγとおくと、以下のように表せます。
△R（回復者数の変化）
＝I（感染者数）×γ（感染者が回復ないし亡くなる確率）
さらに、感染者数（I）は、①未感染者数（S）に、未感染者が感染する確率を乗じた数だけ増え、一方で、②既存の感染者が回復ないし亡くなった数だけ減少します。したがって、以下のように表せます。
△I（感染者数の変化）＝S（未感染者数）×未感染者が感染する確率
―I（感染者数）×γ（感染者が回復ないし亡くなる確率）
周囲に感染者が多いほど、また、ウイルスの感染力が強いほど感染しやすくなります。このことを踏まえ、未感染者（S）と感染者（I）の積に、ウイルスの感染力などを反映する確率（β）を掛けたものを上述の式の右辺の第一項とすると、以下のように表せます。
ΔI（感染者数の変化）＝S（未感染者数）×I（感染者数）× β
―I（感染者数）×γ
なお、ここで回復者（R）としてカウントされている方々には、亡くなられた方々も含まれています。
ここで、
感染者比率（𝑥） =I（感染者数）⁄N（総人口）
回復者比率（𝑦） =R（回復者）⁄N（総人口）
とおくと、未感染者比率＝ 1 − 𝑥 – 𝑦 と表すことができます。
この感染者比率は、前述の通り、未感染者の新規感染、すなわち、
N（1 − 𝑥 − 𝑦）×N𝑥 × β
によって上昇します。また、感染者の回復、すなわち、
N𝑥 × γ
によって低下します。これらをまとめ、わかりやすくするために時間の単位を１/γ日に変換する（→γで除する）と、感染者比率の変化（Δ𝑥）は
感染者比率の変化（△𝑥）=Nβ⁄γ(1 − 𝑥 − 𝑦)𝑥 − 𝑥
と書くことができます。Nβ/γは、「免疫を持たない集団に入り込んだ感染者１人が回復するまでに、他者を何人感染させるか」を示すものであり、「基本再生産数」と呼ばれます。この基本再生産数が１を大きく上回れば、増えた感染者が一段と感染を拡大させることになり、感染が急速に広まります。一方で、これが１を下回れば、計算上、感染は徐々に収束していくことになります。
連載第51回「日本のDXのどこが問題か」（9月8日掲載予定）
